目录
前言
一、树的定义
二、树的若干术语
1.结点的度
2.叶子
3.双亲与孩子
4.兄弟
5.祖先
6.树的度
7.结点的层次
8.树的深度
9.有序树和无序树
10.森林
三、树的逻辑结构
四、树的存储结构
1.顺序存储
2.链式存储
五、二叉树
1.定义
2.二叉树的五种状态
3.树和二叉树之间的转换
1.树转二叉树
2.二叉树转树
前言
这边博客主要是介绍树和二叉树。
一、树的定义
树是由n(n>=0)个结点组成的有限集合T,如果n>0,并且满足两个条件:
- 有且仅有一个结点称为根(root)
- 当n>1的时候,其余的结点分为几个互不相交的有限集合,每个集合本身又是颗树,被称为这个根的子树。
二、树的若干术语
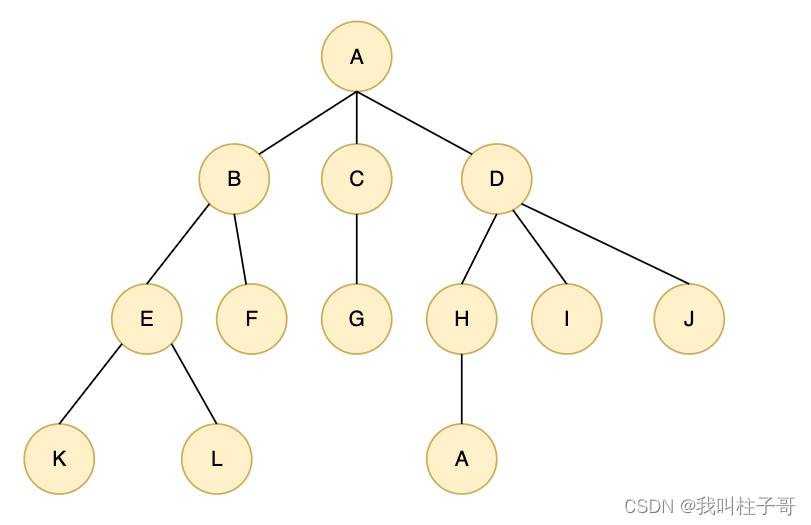
图1.树
1.结点的度
结点的度也就是当前节点的子结点的个数。
例如在上图中A结点的度为3,B结点的度为2,H结点的度为1。
2.叶子
度为0的结点。
3.双亲与孩子
E是B的孩子,E是K和L的父结点
4.兄弟
B、C、D为兄弟结点
5.祖先
M的祖先结点为H、D、A
6.树的度
树中最大结点的度
7.结点的层次
根结点是第一层,根的结点为第二层,依次类推
8.树的深度
树的深度指的是从根节点到树中任意节点的最长路径的长度。换句话说,树的深度是根节点到最深层节点的路径的长度。
9.有序树和无序树
左右结点不能变的树为有序树,反之称为无序树。
10.森林
两个或者两个以上的树组成森林
三、树的逻辑结构
一个结点可能有多个直接后继,但只有一个直接前驱,且子树之间互不相交。
四、树的存储结构
1.顺序存储
按照从上到下、从左到右的顺序存储。
我们在结点和结点的双亲结点的个数存储树的信息。
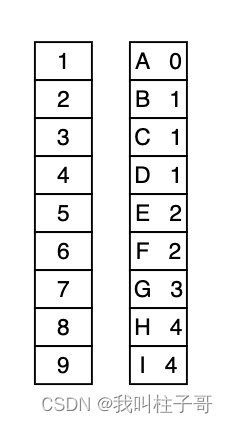
图2.树的顺序存储结构
顺序存储有个缺点:我们需要存储所有的结点信息,当树只有左节点或者右节点的时候,我们需要再顺序表的位置补充好多个空节点,这样会造成存储空间的浪费,而且操作很不方便。依次我们一般使用顺序存储表示完全二叉树。
2.链式存储
我们使用链表存储树。这样也有一个问题,表示树的指针的个数是不确定的。

图3.使用链表存储树
有没有更好的办法呢,答案是有的,我们可以把树转成二叉树来存储。
五、二叉树
1.定义
二叉树或为空树,或是由一个根结点加上两棵分别称为左子树和右子树的互不相交的二叉树组成。
2.二叉树的五种状态

图4.二叉树的五种状态
3.树和二叉树之间的转换
1.树转二叉树
长子作为左孩子节点,兄弟节点作为右结点。
方法:加线(兄弟相连)-- 抹线(长兄为父)--旋转
以图1的树为例。第一步我们把结点的长子作为二叉树的左节点,其余的兄弟结点作为右结点。
操作之后,树的形状为下图5
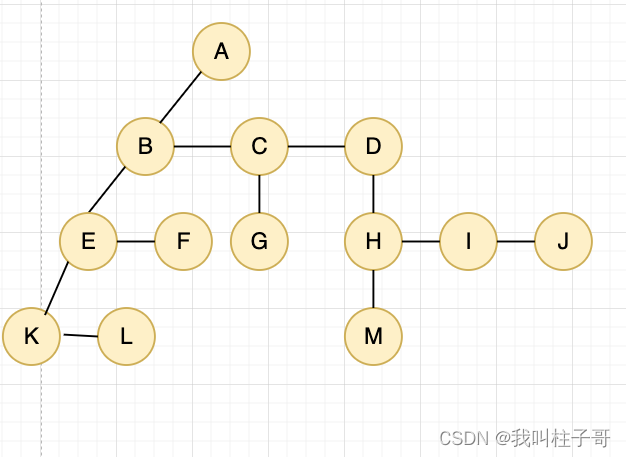
图5.长子作为左结点,兄弟结点作为右结点
然后旋转兄弟结点。旋转之后的二叉树为下图6
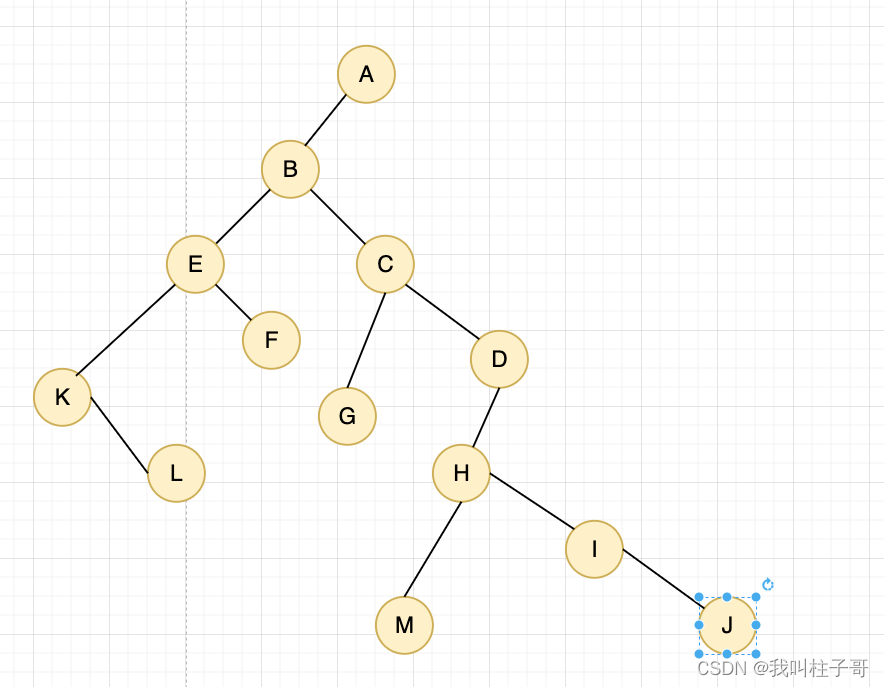
图6.树转二叉树
2.二叉树转树
和上述树转二叉树的顺序相反即可。